Introduction¶

A brief overview of quantum mechanics¶

The following is a brief overview of quantum mechanics, designed to provide you with enough foundational knowledge to begin working with SigSpace. We cover the Schrödinger equation and its connection to wave functions and operators. If you're already familiar with these concepts, feel free to skip ahead to the tutorials section.

What is Quantum Mechanics¶

Quantum mechanics is a fundamental theory that describes the behavior of particles at atomic and subatomic scales. What sets it apart from classical mechanics is the fact that particles exhibit wave-like properties. This is famously demonstrated in the electron double slit experiment:

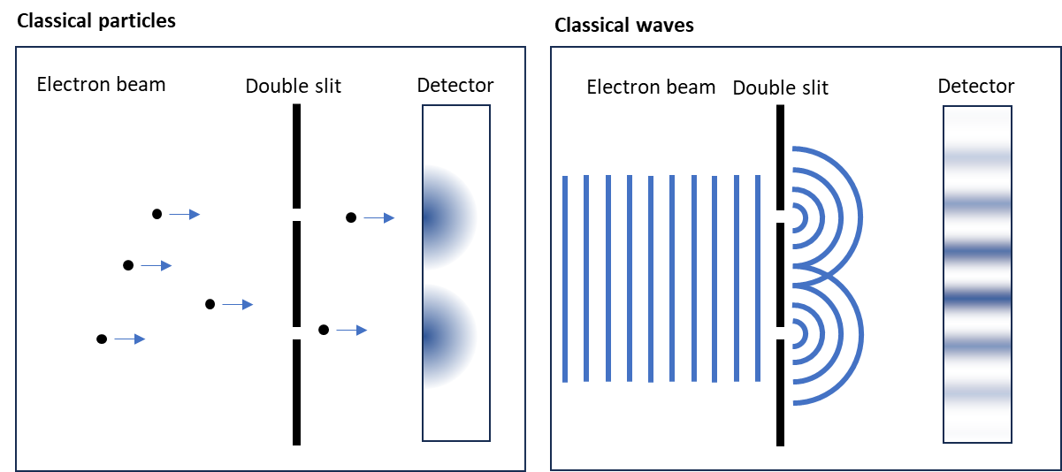
In this experiment, an electron beam is directed at a double slit. According to classical mechanics, one would expect two distinct spots on the detector, corresponding to the two slits. However, what appears instead is a diffraction pattern, indicating that the electrons behave like waves.

To produce such a diffraction pattern, particles must have wave-like characteristics. When two waves intersect, their amplitudes combine as described by the superposition principle. If the amplitudes are in phase (having the same sign), they reinforce each other (constructive interference). If they are out of phase (opposite signs), they cancel each other out (destructive interference). This interaction of waves creates the diffraction pattern observed in the experiment.

However, electrons also display particle-like properties. For instance, their momentum (a classical particle attribute) can be measured in diffraction experiments or scanning tunneling microscopy (STM).

The dual nature of electrons—exhibiting both wave and particle properties depending on the experiment—is known as wave-particle duality.

The quantum state, its operators and the wave function¶

Wave functions are often confused with quantum states, but they are distinct concepts. A quantum state is an abstract mathematical representation of the condition in which a particle exists. By applying operators to a quantum state, measurable quantities such as momentum or position, as well as the particle's wave function, can be derived.

Quantum states can be described using either vectors or wave functions. In SigSpace, we focus on wave functions, as the library calculates them based on a given potential. Wave functions are generally classified into two categories: the ground state (the lowest energy state) and excited states (higher energy levels).

The ground state¶

In the ground state, an electron is at its lowest possible energy. The wave function for this state has no zero crossings, meaning it remains positive or negative throughout. An example is shown in the image below (an example calculation for an attractive potential with $V = -1$ for $|x| < 5$). The wave function reaches its maximum at the center and gradually decays to zero as it approaches the boundaries.

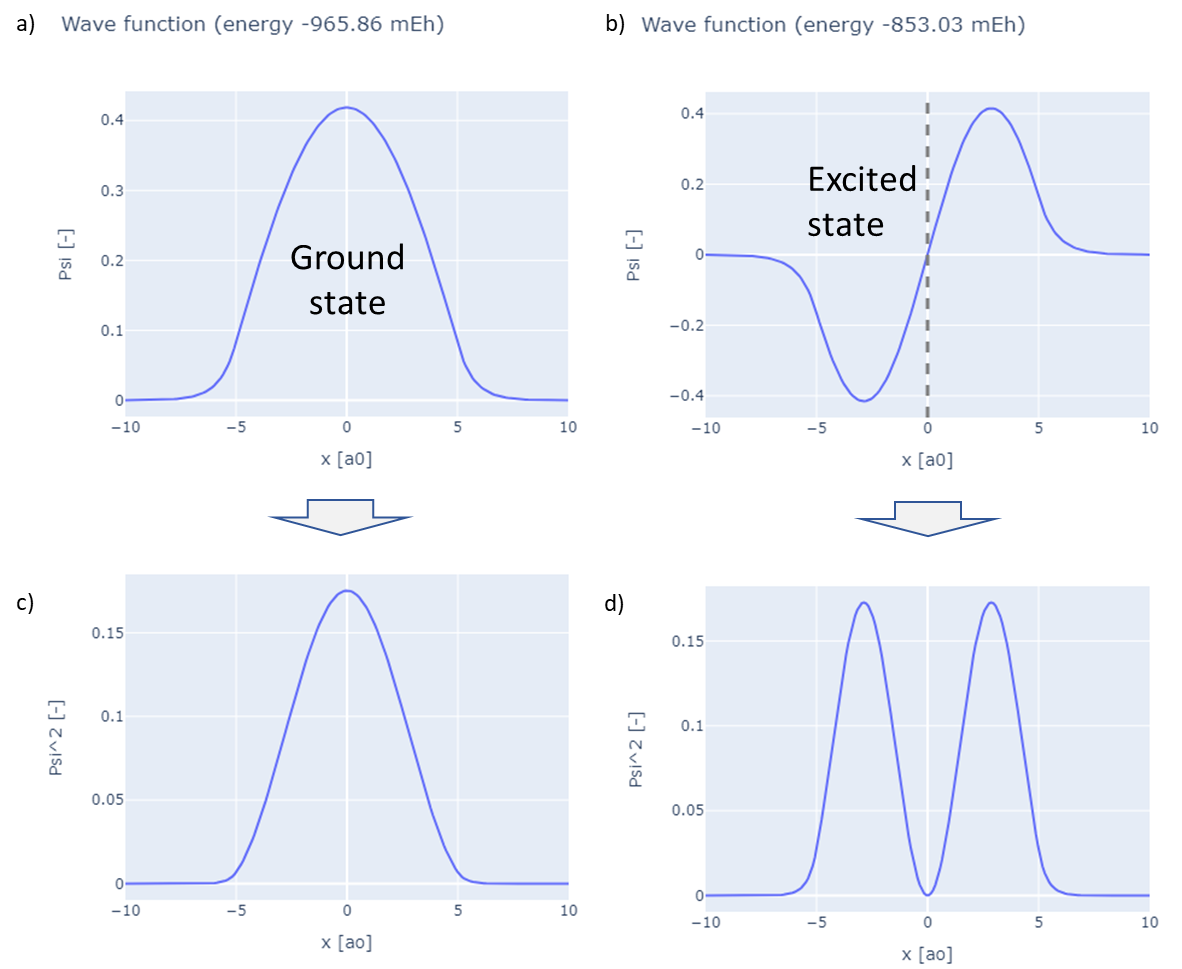
While the wave function itself does not have a direct physical interpretation, its squared amplitude represents the probability density of finding the particle at a specific location. This is illustrated in the panel below. In this example, the highest probability of locating the particle is at the center ($x=0$). If you integrate the squared wave function over the entire space, the result is one, indicating that the particle must exist somewhere. A wave function with this property is called normalized. Not all wave functions are initially normalized, and normalization may be required as a final step in the calculation.

Excited states¶

As illustrated in the figure above, the wave function corresponds to a specific energy. In the figure, the energy is measured in Hartree, a common atomic unit. A negative energy value indicates that the electron is in a bound state. The energy level depends on the shape of the potential. When a state has higher energy then the ground state, it is referred to as an excited state. An example is shown on the right side of the figure, where the wave function exhibits an additional zero crossing at the center. This zero crossing is called a node. The more nodes a wave function has, the higher is the energy.

If the energy becomes positive, the state is no longer bound, and the wave function does not decay to zero at the boundaries. In the excited state, as with the ground state, the probability density is represented by the square of the wave function, as seen in the bottom-right panel.

Operators¶

Operators are mathematical operations that can be applied to quantum states. According to the postulates of quantum mechanics, every measurable physical quantity has a corresponding operator.

Operators often written in what is known as bra-ket notation, which simplifies the integrals involved in quantum mechanical calculations. For example:

\begin{equation} A | \psi \gt = a | \psi \gt \end{equation}

where $ A $ is an operator applied to the quantum state $ | \psi > $, resulting in the same state multiplied by a factor $a$. The value $a$ is the eigenvalue of the operator, which corresponds to a measurable physical quantity. Common operators include those for momentum, position and energy.

For more details about operators and how to work with them in SigSpace, refer to the bra-ket tutorial.

The Schrödinger equation ¶

The operator for energy is known as the Hamiltonian operator. When substituted into the equation, it yields the Schrödinger equation:

\begin{equation} {\cal H} \Psi = E \Psi \end{equation}

In this equation, $E$ represents the energy of the resulting state. The Schrödinger equation applies to particles like protons bosons) and electrons (fermions). In the following, we will focus on electrons, as they play a crucial role in determining many material properties.

The Hamiltonian operator is defined as:

\begin{equation} {\cal H} = -0.5 \cdot \Delta + V \quad \quad \textrm{with} \quad \Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \end{equation}

where $ \Delta $ is the Laplace operator, representing the sum of second derivatives in all spatial directions. The potential $ V $ can either attract (negative potential) or repel (positive potential) electrons, depending on the nature of the problem. For instance, attractive potentials often originate from nuclei, which draw in electrons, while repulsive potentials typically result from electron-electron interactions due to their identical charges.

Since all terms in the stationary Schrödinger equation are real, the resulting wave function should also be real. This is important to note because, in general, solutions to the Schrödinger equation can be complex-valued.

Ongoing literature¶

Follow to the tutorials to see some examples on how to use SigSpace.